Воскресенье, 13.07.2025, 08:13

Блог Холодильника

Главная | Регистрация | Вход

Приветствую Вас Гость
RSS

Тэги

Опрос

Статистика

Онлайн всего: 1

Гостей: 1

Пользователей: 0

Форма входа

Поиск

Календарь

Архив записей

Балалайка

Главная » » билет номер 2

билет номер 2

17:43

Электрическое поле — особый вид материи, существующий вокруг тел или частиц, обладающих электрическим зарядом, а также в свободном виде при изменении магнитного поля (например, в электромагнитных волнах). Для количественного определения электрического поля вводится силовая характеристика - напряженность электрического поля. Напряженностью электрического поля называют векторную физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещённый в данную точку пространства, к величине этого заряда. Направление вектора совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд.

Сила Лоренца описывает воздействие электромагнитного поля на частицу.

Эффект поля заключается в том, что при воздействии электрического поля на поверхность электропроводящей среды в её приповерхностном слое изменяется концентрация свободных носителей заряда. Этот эффект лежит в основе работы полевых транзисторов.

Основным действием электрического поля является силовое воздействие на неподвижные (относительно наблюдателя) электрически заряженные тела или частицы. Если заряженное тело фиксировано в пространстве, то оно под действием силы не ускоряется. На движущиеся заряды силовое воздействие оказывает и магнитное поле (вторая составляющая силы Лоренца).

Напряженность...

Напряженностью электрического поля в данной точке пространства называется величина, равная отношению силы F, действующей на единичный положительный заряд q, помещенный в данную точку, к величине этого заряда.

E = F/q.
(E = F при q = 1).

Для взаимодействия точечных зарядов справедлив закон Кулона. Следовательно,

E = F/q = Q/(4pee₀r²)*r/r,

где Q - заряд, создающий поле,
e - диэлектрическая проницаемость среды.

Пробным зарядом называется тело, величина заряда которого настолько мала, что не искажает свойства исследуемого поля. Его величина равняется минимальному заряду, обнаруженному в природе, q = 1.6*10^-19 Кл.

Единицы измерения напряженности с системе СИ [E]: 1 В/м = 1 Дж/(м*Кл) = 1 Н/м.

Поскольку сила и напряженность поля - есть пропорциональные величины F = q*E, то для напряженности электрических полей справедлив принцип суперпозиции (см.рис.1).

E = E₁ + E₂ + E₃ + E_i + … + E_n,

т.е. напряженность поля системы n зарядов равна векторной сумме напряженностей полей, создаваемых каждым из зарядов системы в рассматриваемой точке.

Принцип суперпозиции отражает независимость действия электростатических полей.

Силовые линии электрического поля

Силовые линии электрического поля - воображаемые линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности электрического поля в этой точке.

Силовые линии электрического поля начинаются на положительных и заканчиваются на отрицательных зарядах.

Силовые линии электрического поля не пересекаются.

Напряженность поля точечного заряда.

Обозначим: q - заряд, создающий поле,

q₀ - заряд, помещенный в поле (внешний заряд).

Закон Кулона: . Напряженность поля: .

Тогда напряженность поля точечного заряда:

Напряжённость электрического поля точечного заряда

[править] Для системы СИ

Используя потенциал

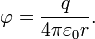Вектор $\vec E$ выражается как градиент потенциала, взятый с обратным знаком: $\vec E = - \nabla \varphi.$ К примеру, для точечного заряда, исходя из закона Кулона $\varphi = \frac{q}{4 \pi \varepsilon_0 r}.$ Так как эквипотенциальные поверхности являются в этом случае сферами, то производная по нормали есть производная по радиусу. Таким образом мы можем прийти к так называемому кулоновскому полю:

$\vec E = - \frac{\partial \varphi}{\partial n}= -\frac{\partial }{\partial r } \left( \frac{q}{4 \pi \varepsilon_0 r} \right) = \frac{q}{ 4 \pi \varepsilon_0 r^3} \vec r$ .

Используя теорему Остроградского — Гаусса

Из формулы Остроградского-Гаусса вектор $\vec E$ можно определить, зная плотность распределения зарядов. Согласно формуле Гаусса — Остроградского, а также используя уравнение Максвелла $\operatorname{div}{\vec E}= \tfrac{\rho}{\varepsilon_0}$ , легко получить:

$\oint\limits_S \vec{E} \cdot \mathrm{d}\vec{S} = \int\limits_V \operatorname{div}{\vec E} \mathrm{d}V = \frac{1}{\varepsilon_0} \int\limits_V \rho \mathrm{d}V = \frac{q_{in}}{\varepsilon_0},$

где q_in — заряд, находящийся внутри замкнутой поверхности S, объемом V. В качестве поверхности интегрирования возьмем сферу (центральная симметрия), тогда

$\oint\limits_S \vec{E} \cdot \mathrm{d}\vec{S} =E \oint\limits_S \mathrm{d}\vec{S} =E \cdot 4 \pi r^2$

В силу центральной симметрии поля точечного заряда:

$E = \frac{q}{4 \pi \varepsilon_0 r^2}$ .

Как и следовало ожидать, результаты полностью совпали.

[править] Для системы СГС

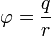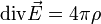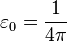Рассуждения аналогичны, вся разница лишь в том, что изменяется вид потенциала $\varphi = \frac{q}{r}$ , уравнение Максвелла $\operatorname{div}{\vec E}=4 \pi \rho$ и $\varepsilon_0 = \frac{1}{4 \pi}$ . В итоге, получаем в системе СГС:

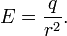
$E = \frac{q}{r^2}.$

Просмотров: 938 | Добавил: Grohot | Рейтинг: 0.0/0 |

Всего комментариев: 0